[日商簿記1級]線形計画法



経理で用いられる数学の考え方の一つに、線形計画法(リニアー・プログラミング)があります。
名前だけ見ると少々難しそうですが、実態はそうでもありません。具体的な流れを見ていきましょう。
線形計画法
線形計画法は主に、製品が2種類(仮にAとBとする)あり、それを作成するための「機械の稼働時間」や、「作業時間」など、二つ以上の条件下でどのくらいの割合で生産すれば一番利益を上げられるかを、1次式を用いて考える方法です。
ここで線形計画法を用いるには、三つの要素である、目的関数・制約条件・非負条件を考える必要があります。
目的関数
目的関数は、最大にするべき利益を求めるための関数です。
例えば、製品Aを1個売り上げたときの利益が240円、製品Bの利益が200円、合計の利益をZとするなら、以下のようになります。
制約条件
制約条件は、各製品を作るための環境や制約などの条件を不等式で示したものです。
製品Aを一つ作るのに、機械稼働時間が4時間、Bの場合2時間かかるとして、合計で機械稼働時間が年間2,000時間までしか動かせない場合、以下のようになります。
個数上の制約がある場合、その条件も組み込んでやる必要があります。例えばAが440個、Bが360個までしか需要がない場合、以下の式を加えます。
非負条件
非負条件とは、製品を生産する個数がマイナスにならないということです。
そもそも、今年度の製品の生産は-1個だったとか言われても意味がわからず、あり得ない話です。不等式にあらわすと以下のとおりになります。
\[B \geq 0\]
問題
ある会社では、2種類の製品A、Bを、材料は機械で加工し、その後人力で組立作業をして製造・販売しています。今年度の資料は以下のとおりで、この条件に基づいて次年度以降、それぞれいくつずつ製品を作ればよいかそれぞれの個数を求め、そのときの年間の利益も求めなさい。
| 製品A | 製品B | |
| 1個あたりの利益 | 240円 | 200円 |
| 1個あたりの機械時間 | 4時間 | 2時間 |
| 1個あたりの組立時間 | 2時間 | 4時間 |
| 最大需要量 | 440個 | 360個 |
なお、年間の機械稼動時間は2000時間、年間の組立作業時間は1600時間とします。
解説
線形計画法を用いて考える場合は、まずそれぞれの式をグラフに落とし込み、そこから範囲を絞っていくことが重要になります。

目的関数は最終的な利益を求めるための式のため、グラフ上には表さず、それぞれの条件をグラフに書き込んでいきます。
横軸をA、縦軸をBとし、先ほどの条件の
\(4A + 2B \leq 2000\)・・・(1)
\(2A + 4B \leq 1600\)・・・(2)
\(A \leq 440\)・・・(3)
\(B \leq 360\)・・・(4)
\(A \geq 0\)・・・(5)
\(B \geq 0\)・・・(6)
をそれぞれグラフに書き込んでみましょう。グラフに書き込む際に、分かりやすいよう不等式を等式として書き込んでいます。また、(5)(6)については正の範囲を見ればよいだけなので割愛します。
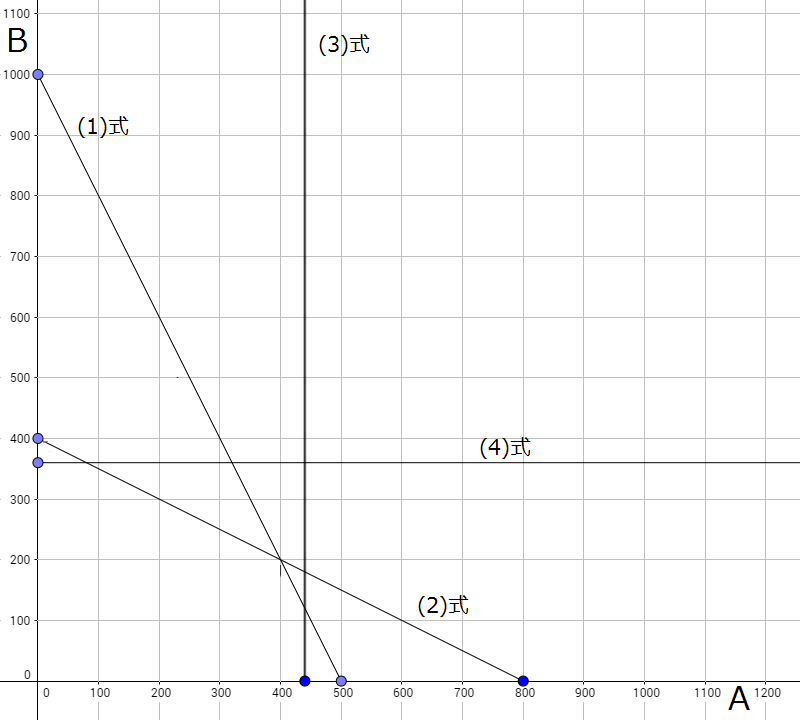
次に共通の範囲内のそれぞれの交点に着目します。
共通の範囲とは下図のように橙色に示した範囲を言い、すべての式の条件に当てはまる範囲を表しています。
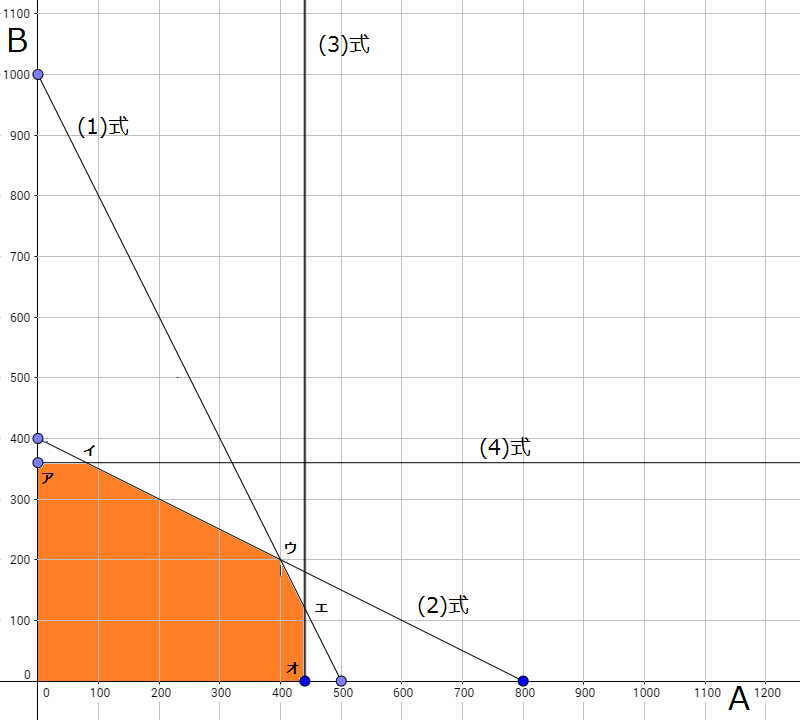
ちなみにこの図のように、凹んでいない部分の集合を凸集合と呼び、その端の点を端点といいます。
要するに共通の範囲内のそれぞれの交点が端点です。
原点\((0,0)\)から遠ざかれば遠ざかるほど、製品A、Bの販売量は増えていき、利益も増えていきます。
したがって、利益が最大になるのは、この範囲内の端点のいずれかということになります。
では、それぞれの端点の座標を求めてみましょう。ここでも、それぞれの不等式を等式と見て扱います。
ア:(4)式\(B = 360\)とB軸上の交点
イ:(2)式\(2A + 4B = 1600\)と(4)式\(B = 360\)の交点
ウ:(1)式\(4A + 2B = 2000\)と(2)式\(2A + 4B = 1600\)の交点
エ:(1)式\(4A + 2B = 2000\)と(3)式\(A = 440\)の交点
オ:(3)式\(A = 440\)とA軸上の交点
となります。アとオに関してはそれぞれの軸上なのでアは\((0,360)\)、オは\((440,0)\)となります。
イとエに関してはそれぞれイの(2)式に\(B = 360\)を、エの(1)式に\(A = 440\)を代入すればよく、その座標はイは\((80,360)\)、エは\((440,120)\)となります。
ウの交点は少しめんどくさいですが、以下の連立方程式を解くことで交点が求まります。
\begin{eqnarray} \left\{ \begin{array}{l} 4A + 2B = 2000 \\ 2A + 4B = 1600 \end{array} \right. \end{eqnarray}
これを解くとウは(400,200)となります。
表にまとめると以下のようになります。
| A | B | |
| ア | 0個 | 360個 |
| イ | 80個 | 360個 |
| ウ | 400個 | 200個 |
| エ | 440個 | 120個 |
| オ | 440個 | 0個 |
あとはそれぞれの製造した個数(=売り上げ個数)にAは1個あたり利益240円、Bは利益200円なので、それぞれの個数を掛けて、最後にAとBの利益の合計を求めれば答えが得られます。
この先は利益を求めるために一つ一つ計算して当てはめなければなりませんが、イはアよりも、エはオよりも売り上げる個数が多いことは表を見れば明らかなため、検証するのはイ、ウ、エのみで問題ありません。
イ:\(240 \times 80 + 200 \times 360 = 91200\)より、92,000円
ウ:\(240 \times 400 + 200 \times 200 = 136000\)より、136,000円
エ:\(240 \times 440 + 200 \times 120 = 129600\)より、129,600円
これより、ウが一番利益が高くなるため、Aを400個、Bを200個売ったときが最大の利益になることが分かります。
解答
A:400個、B:200個、利益:136,000円
線形計画法・まとめ


線形計画法と聞くと難しく身構えてしまいがちですが、やっていることは1次式のグラフの交点を求め、それぞれの場合を試しているだけに過ぎません。
また、条件が二つの場合は大抵軸と平行線と交わる端点ではなく、連立方程式を解いた場合が最適解になることが多いです。

福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など





ディスカッション
コメント一覧
まだ、コメントがありません